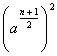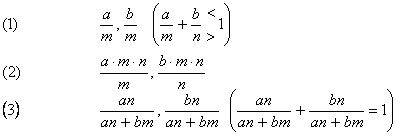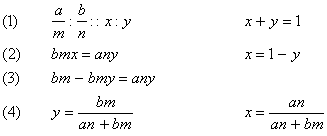603

In the progression a (a + 1) (a + 2) (a + 3) ... (a + n), if x is the distance from the first or last number, we get:

a+ (a + n) = (a + x) + (a + n – x).

604

In the progression a (a + 1) (a + 2) (a + 3) ... (a + 2n), then

a + (a + 2n) = 2 (a + n).

In the progression 2a (2a + 2)(2a + 4)(2a + 6) ... (2a + 2n), then

2a + (2a + 2n) = 2 (2a + n).

In the progression (2a + 1) (2a + 3) (2a + 5) (2a + 7) ... (2a + [2n + 1]), then

(2a + 1) + (2a + [2n + i]) = 2 (2a + [n + 1]).

605

In the progression , if x is the distance from the first or last number, we get:

.

In the progression , if x is the distance from the first or last number, we get:

.

606

In the progression a a² a³ a⁴ ∙ ∙ ∙ aⁿ, then

a∙aⁿ =

607

Cf. al-Khuwarizmi, Mafatih al-`ulum (Cairo, 1349/1930), p. III; al-Biruni, Kitab at-tafhim, ed. and tr. R. R. Wright (London, 1934), pp. 29 f. As al-Khuwirizmi explains it, a muthallathah results from adding the num­bers from one on; a murabba'ah results from adding every second number (or from adding up the adjacent numbers of a muthallathah); a mukhammasah results from adding every third number; a musaddasah from adding every fourth; and so on.

Thus, the progression 1 2 3 4 5 6 7 8 9 10 11 12 13 . . . yields the muthallathah 1 3 6 10 15 21 28 and so on. The progression 1 3 5 7 9 11 13 . . . yields the murabba'ah 1 4 9 16 25 36 49 and so on. The progression 1 4 7 10 13 . . . yields the mukhammasah 1 5 12 22 35 and so on. The progression 1 5 9 13 . . . yields the musaddasah 1 6 15 28 and so on.

Ibn Khaldun, however, proceeds in a slightly different manner. He always adds a muthallathah to a given progression, in order to obtain the next higher one. Thus, he has:

A perusal of the largely unpublished Arabic literature on arithmetic will certainly provide an exact presentation of the table that Ibn Khaldun has in mind. The theory of polygonal numbers (as well as all the other theorems mentioned in this section) came to the Arabs through the work of Nicomachus of Gerasa, which was translated into Arabic and is preserved but not yet published in its Arabic form. However, though Ibn Khaldun seems to refer to the geometrical figures of Nicomachus, which provided the terminology for the subject, his table would appear to be one made up of numerical pro es­sions. Cf. Nicomachus Introduction to. Arithmetic ii. 8-11. M. L. D'Ooge(tr.), (University of Michigan Studies, Humanistic Series, No. 16) (New York, 1926), pp. 241 ff. [* Ar. translation, ed. W. Kutsch (Beirut, 1959)].

608

Actually, a new sentence should begin here ("By adding them up, a triangle is formed"), but the text does not permit such a construction, and no correction is permissible.

609

That is, 2 (2n + 1).

610

That is, 2 (m + 1) (2n + 1).

In literal translation, the Arabic terms, derived from the Greek, read: even, odd, evenly-even, unevenly-even, and evenly-even-odd. Ibn Khaldun does not mention oddly-odd, i.e., odd numbers multiplied by each other:

(2n + 1)(2n + 1).

Cf. al-Biruni, op. cit., p. 25.

611

That is, in theoretical mathematics.

612

Cf. 1:238, above, and pp. 123 and 137, below.

613

Ibn Khaldun is said to have written a work on the subject himself; cf. 1:xliv, above. The first two paragraphs of this section are quoted by J. Ruska, "Zur iiltesten arabischen Algebra and Rechenkunst," in Sitzungs­berichte der Heidelberger Akademie der Wissenschaften, Philos.-hist. Kl. (Heidelberg, 1917), pp. 19 f.

614

615

The word mabsul as such can also mean "extensive," but in view of the character of the work, Renaud (see n. 616, below) suggests the above transla­tion.

616

Muhammad b. 'Abdallah b. 'Ayyash. Cf. GAL, Suppl., II, 363; and esp., H. P. J. Renaud, "Sur un passage d'Ibn Khaldun relatif a l'histoire des mathematiques," Hespiris, XXXI,(1944), 35-47, where Renaud corrects statements he had made earlier in Hespiris, XXV (1988), 24 (n. 6). Renaud shows that a large work by al-Hassar, whose existence we should expect from Ibn Khaldun's reference to the "small" work, actually did exist.

617

The work referred to is Ibn al-Banna"s well-known Talkhis a'mal al-hisab.

618

At the beginning of the Raf , Ibn al-Banna' states that the work was intended to "explain the scientific contents and comment on" the apparent difficulties of the Talkhis. Cf. MS. or., Princeton, 1092-A (80 B).

619

The pronoun found in the Arabic text must refer to the Raf , but the statement would seem to apply rather to the Talkhis.

620

The following eight lines are not found in Bulaq, and in A they are still in the form of a marginal note. There is no reference in Ibn al-Banna"s works to the effect that he used the sources mentioned. However, it is clear from Ibn Khaldun's attitude toward Ibn al-Banna' that he would not think of accusing him of plagiarism.

621

Mubammad b. 'Isa b. 'Abd-al-Mun'im, who lived at .the court of Roger II of Sicily. Cf. H. P. J. Renaud in Hespiris, XXV (1938), 88-85. Nothing is known about al-Abdab and his work.

622

The translation follows that suggested by Renaud in Hespiris, XXXI (1944), 42 f.

623

Cf. Qur'an 24.35 (35).

624

Adad: i.e., n, the part of the equation that is not a multiple (or fraction) of the unknown.

625

Shay': Latin res, that is, x (the unknown).

626

Mal: Latin substantia, census, that is, x².

627

That is, the higher powers are expressed by multiplying two or more times the second and third (ka'b "cube," not mentioned by Ibn Khaldun) powers. Thus, x⁴ is mal mal, x⁵ is mal ka'b, etc. For uss, cf. P. Luckey, Die Rechenkunst bei Gamssid b. Mas'ud al-Kasi (Abhandlungen fur die Kunde des Morgenlandes, No. 31') (Wiesbaden, 1951), pp. 59, 70 f., 104 f. According to Luckey, uss has two meanings, that of exponent, and another referring to the position of the numbers (one for the units, two for the tens, three for the hundreds, etc.). Cf. also 1:241, above, and pp. 203 ff., below.

628

Jabr, hence Algebra.

629

I.e., n, x, x³, and the three basic equations: ax = n , bx² = n , and ax² = bx. Cf. L. C. Karpinski, "Robert of Chester's Translation of the Algebra of al-Khowarizmi," in Contributions to the History of Science (University of Michigan Studies, Humanistic Series, No. 11) (Ann Arbor, 1930), p. 69.

630

ax = n; bx² = nx

631

x² = bx; x = b, b being the multiple of the "root."

632

633

Apparently, ax³ + bx² = cx + n , or the like.

634

The simple equations are: ax = n; bx2 = n; and ax² = bx. The composite equations are: ax² + bx = n; ax² + n = bx; and ax² = bx + n. Cf. Karpinski, op. cit., pp. 69 and 71.

635

Muhammad b. Musa, who lived in the first half of the ninth century. Cf. GAL, 1, 215 f.; Suppl., I, 381 f.

636

Ca. 900? Cf. GAL, Suppl., I, 390.

637

He is referred to as Abul-Qasim al-Qurashi of Bougie, and was a source of Ibn al-Banni's Talkhis. Cf. H. P. J. Renaud in Hespiris, XXV (1938), 35-37.

638

Cf. 'Umar al-Khayyam, Algebra, ed. F. Woepcke (Paris, 1851).

639

Qur'an 35.1 (1).

640

I.e., calculation (elementary arithmetic) and algebra.

641

Ali b. Sulayman. Cf. Sa'id al-Andalusi, Tabaqat al-umam, tr. R.

Blachere (Publications de l'Institut des Hautes Etudes Marocaines, No. 28)

(Paris, 1935), pp. 131 f.

642

Agbagh b. Mubammad, d. 426 [979-1035]. Cf. GAL, 1, 472; Suppl.,

I, 861; Sa'id al-Andalusi, Tabaqdt, pp. 13o f., where his age is incorrectly

given as fifty (instead of fifty-six) solar years.

643

'Amr ('Umar?) b. Ahmad, d. 449 [1057/58], a member of Ibn Khal­dun's family. Cf. Sa'id al-Andalusi, Tabaqdt, p. 133, and above, 1:xxxiv. Ibn Fadlallih al-'Umarl, d. 749 [1349], states in his Masdlik al-abdr that he had seen very good astrolabes signed by Ibn Khaldun, and had personally copied a work of his, which, however, he lost later on. ( MS, Topkapusaray, Ahmet III, 2797, Vol. V, p. 417.)

644

The subject was treated as a part of jurisprudence, pp. 20 ff., above.

645

In such cases, the process called 'awl "reduction," mentioned below, is applied. The total of the inheritance shares, as stipulated by the Qur'an, may be greater than the entire estate. Thus, according to the famous example, if a man leaves two daughters, his two parents, and one wife, the daughters would be entitled to two-thirds, the parents to one-third, and the wife to one­eighth of the estate. Qur'an 4.11 f. (12-14). Therefore, the following pro­cedure is used. The fractions are reduced to their common denominator: the new numerators are added up (16 + 8 + 3 = 27); and the total is made the new denominator. Thus, the new shares are The wife's share, which was one-eighth, is "reduced" ('awl) to one-ninth, but the proportion of the shares to each other is preserved.

In our symbols, the procedure can be expressed as follows (for the sake of simplicity only two fractions are assumed):

The correctness of the procedure can be proven as follows:

646

Sic C and D.

647

Cf p. 22, above. 128

648

All these scholars were mentioned above, p. 21. This passage was used by Hajji Khalifah, Kashf az zunun, ed. Flugel (Leipzig & London, 1835-58), III, 64.

649

This Berber name is spelled with a ,s into which a small z is inserted. Cf. 1:67 (n. 183), above. He is 'Abdallah b. Abi Bakr b. Yahya, who was born ca. 643 [1245/46] and who was still alive in 699 [1299/1300]. Cf. Ahmad Baba, Nayl al-ibtihaj (Cairo, 1951/1932, in the margin of Ibn Farhun, Dibaj), pp. 14.0 f.

650

Cf. the Autobiography, pp. 31 f.

651

This remark would seem to imply that Hanafite and Hanbalite works are inferior.

652

Cf. Qur'an 2.142 (136), 213 (209), etc.